Introduction à la calculatrice de transformation de Laplace
Vous pouvez utiliser une calculatrice de transformation de Laplace en ligne avec des étapes pour la conversion d'une fonction à valeur réelle en une fonction à valeur complexe. En ingénierie et en recherche, la transformation de Laplace est utilisée pour analyser les systèmes de contrôle et les appareils électroniques.
La calculatrice de Laplace peut également être utilisée pour résoudre des équations différentielles à l'aide de l'équation de la transformation de Laplace. Poursuivez votre lecture pour en savoir plus sur les transformations de Laplace et la calculatrice d'intégrales de Laplace.
En savoir plus : Ce site web vous aide à apprendre les calculs concernant les intégrales doubles et triples. Vous pouvez trouver une calculatrice d'intégrales multivariables et une calculatrice d'intégrales de volume pour des calculs précis d'intégrales doubles et triples.
Qu'est-ce que la transformation de Laplace ?
Les transformations de Laplace décrivent les transformations intégrales en calcul qui convertissent une fonction à valeur réelle f (t) en une fonction à valeur complexe. Cette transformation est utilisée pour convertir des équations différentielles normales en équations algébriques qui peuvent être utilisées pour résoudre des problèmes différentiels ordinaires.
Une équation différentielle linéaire est assez courante dans la pratique, et elle apparaît fréquemment dans les problèmes d'ingénierie électrique, de physique et de systèmes de contrôle. Par ailleurs, la calculatrice de Laplace avec échelons ne peut effectuer que des transformations de Laplace régulières, également connues sous le nom de transformations de Laplace unilatérales.
En effet, un seul côté de la transformée de Laplace (le côté ordinaire) est utilisé et le côté de la transformée de Laplace inverse n'est pas utilisé. Une calculatrice d'intégrales par parties, en revanche, peut être utilisée pour calculer les intégrales de fonctions portant sur des variables concernées.
Voir aussi : Vous pouvez également trouver une calculatrice d'intégrale indéfinie et une calculatrice d'intégrale définie pour trouver l'intégrale définie en ligne.
Formule utilisée par la calculatrice de Laplace
La calculatrice d'intégrale de la transformée de Laplace utilise la formule suivante pour calculer et fournir des résultats précis.
$ F(s) \;=\ ; \int_0^{+∞} f(t) \ ;.\ ; e^{-st}.dt $
Comment fonctionne la calculatrice de transformation de Laplace ?
La calculatrice de transformation de Laplace inverse fonctionne en ligne. Elle nécessite une entrée de la part de l'utilisateur et, grâce à sa méthode de transformation, vous pouvez transformer des fonctions réelles en fonctions complexes. La calculatrice de transformation de Laplace calcule rapidement les résultats sous forme d'étapes, de tracés, de graphiques, etc.
Il existe d'autres calculatrices utiles que vous pouvez utiliser sur ce site Web, comme la calculatrice de coque cylindrique et la calculatrice d'intégrale de rondelle pour la méthode de rondelle.
Comment utiliser la calculatrice d'intégrale de Laplace ?
Il est très facile d'utiliser la calculatrice de transformée de Laplace. Il vous suffit de suivre les étapes ci-dessous pour obtenir des résultats précis.
Étape 1 : Dans le champ de saisie, tapez la fonction, la variable de fonction et la variable de transformation.
Étape 2 : Cliquez sur "Charger un exemple" pour calculer un autre exemple (facultatif).
Étape 3 : Pour acquérir la transformation intégrale, cliquez sur le bouton "Calculer".
La calculatrice laplace affichera les résultats comme suit :
- Tout d'abord, la calculatrice de transformation laplace avec solution pas à pas affiche votre entrée sous la forme d'une équation différentielle ordinaire.
- Ensuite, sous forme algébrique, elle affiche la réponse à l'équation.
- Elle affiche également des tracés de fonctions algébriques données.
Vous trouverez également sur ce site d'autres outils d'intégration en ligne, comme la calculatrice de disques et la calculatrice de transformée sinusoïdale de Fourier, qui vous seront d'une grande aide pour vos calculs en ligne.
Comment résoudre une question avec la calculatrice de Laplace ?
Pour résoudre cette question, vous devrez fournir les valeurs de votre fonction dans l'entrée de la calculatrice de transformée de Laplace, étape par étape.
L'entrée est la suivante
$ L_t \left[ t^4 \ ; sin(t) \right] (s) $
Résultat :
$ \frac{24 (5s^4 - 10s^2 + 1)} {(s^2 + 1)^5} $
Tracé
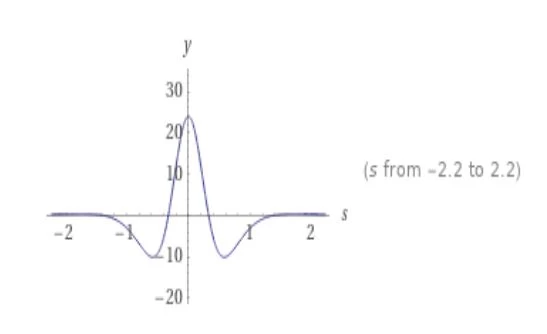
Tracé
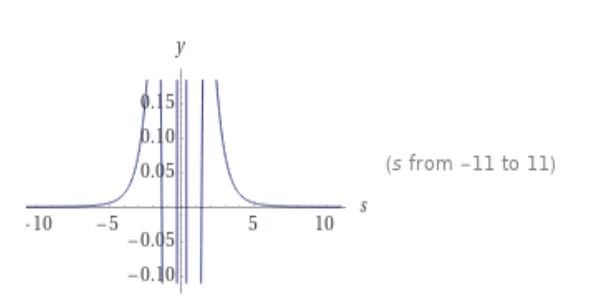
Vous trouverez sur ce site des blogs utiles. Cliquez ici pour en savoir plus sur l'intégrale de fraction et l'importance du calcul intégral.
Conclusion
Essayez cette calculatrice de transformée de laplace avec étapes pour voir comment une équation différentielle ordinaire réelle est transformée en une expression algébrique complexe. Vous pouvez certainement effectuer tous ces calculs correctement, mais il s'agit d'une opération difficile et qui prend du temps. Par conséquent, les étudiants et les professionnels peuvent calculer rapidement à l'aide de cette calculatrice de transformation de laplace.
En savoir plus : Apprenez également à intégrer à l'aide d'une calculatrice et à comprendre quelle méthode utiliser pour trouver le volume d'un solide de révolution.
Autres outils utiles
calculatrice de l'aire entre les courbes
calculatrice de la formule de la règle de Simpson
calculatrice de l'intégration des longueurs d'arc
calculatrice de la longueur d'arc des courbes polaires
calculatrice de l'imite de la somme avec étapes
Questions fréquemment posées
Quel est l'objectif principal de la transformée de Laplace ?
La transformée de Laplace est utilisée pour résoudre des équations différentielles. L'objectif principal de la transformée de Laplace est de convertir les équations différentielles ordinaires (ODE) en variables algébriques. Cette conversion permet de résoudre simplement les EDO.
Le processus de conversion des équations différentielles ordinaires en variables algébriques est délicat en raison de la longueur des calculs manuels. Mais la calculatrice de transformée de Laplace, étape par étape, rend le processus plus facile pour les étudiants de tout niveau.
Peut-on résoudre une équation différentielle à l'aide de la calculatrice de transformée de Laplace ?
Oui, cette calculatrice d'équation différentielle de Laplace vous aide à calculer votre requête et vous fournit les étapes et le graphique.
Quelles sont les utilisations les plus courantes de la transformée de Laplace ?
Voici quelques-unes des utilisations les plus courantes de la transformée de Laplace avec les étapes. Ces avantages de la transformée de Laplace sont également disponibles dans la calculatrice de transformée de Laplace avec une solution pas à pas :
- Il est utilisé pour résoudre les équations différentielles.
- Il est utilisé dans de nombreux domaines de la physique, notamment pour dériver le circuit.
- Il est utilisé dans les circuits intégrés.
- Elle est utilisée dans les systèmes de contrôle pour maintenir la fréquence de la charge.
Quelle est la différence entre la transformation de Fourier et la transformation de Laplace ?
La transformée de Fourier modifie les amplitudes d'un signal en décomposant une fonction qui dépend de l'emplacement ou du temps.
La transformée de Laplace, quant à elle, modifie l'amplitude et les portions d'oscillation qui peuvent être calculées en utilisant la calculatrice de transformée de Laplace avec des étapes gratuites. L'ensemble principal de la transformée de Fourier est la transformée de Laplace.
Qu'est-ce que la transformée de Laplace et pourquoi est-elle importante?
Lorsque des conditions de base sont données, telles que des nombres initiaux nuls, la transformée de Laplace peut être utilisée pour trouver des formes spécifiques de problèmes différentiels.
Nous espérons que cette calculatrice de transformée de Laplace avec solutions vous a aidé dans votre travail. Cette calculatrice de transformée de Laplace inverse a été conçue uniquement pour vous aider, et votre appréciation nous serait très précieuse.

















 jeu de Google
jeu de Google
 Magasin dapplications
Magasin dapplications

0 Comment