In a previous article, we discussed how to find the volume of a solid of revolution by integration. We did that by calculating the area under a curve by running a line segment of varying lengths across the region. We added them all up to get the volume. We just ran some areas across the shape and added all of those up.
Sometimes it is the area of a disc and sometimes the area of a washer. But whatever the situation, we were able to calculate the area of a cross-section rather easily given the functions involved.
Why is the Shell Method?
Shell method is always rotating about the y axis. If we rotate something about the y axis, we get a proper subject. In the shell method, we take a region and rotate it about the y axis to find a cross section.
So in the shell method, we break the region and find the cross sectional area first. Rotation of the cross section helps us to identify the outside and inside radius of the circle. If we have more cross sections, it is likely that we’ll get a better approximation of the volume.
Other method to calculate solid of revolution
Sometimes it is not easy to use the shell method to calculate the solid of revolution. Before jumping on to calculating the solid of revolutions using the shell method, let's look at other alternatives. Below is an example where another method will be a better approach for calculating solid of volume of revolution.
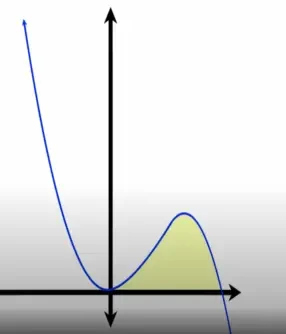
Take an example y = 2x2-x3 and x-axis[0,2], when rotated along the y-axis.
The region between this function and the x-axis looks like this:
Let's assume that we rotate this area around the y-axis to get a solid of revolution. A cross-section of this solid would be a washer given the empty middle region. We can then push it upwards from the base to the top of the solid.
But the problem is that when we did this before the functions were simple like y = x or y x2. Given that we are doing things in terms of “y” and in previous methods we rewrite functions in terms of “y” so that we could integrate.
With the other examples that ended up being no problem and we were able to get expressions for the inner and outer radii of the washer that we could integrate. Here it's not so easy.
Rather than one function per radius here both the radii depend on this same function and furthermore solving this function for “x” in terms of “y” is not a very appealing task.
The Formula for Shell Method
But there is another technique we can try and it is called the method of cylindrical shells. Before we apply this to the problem at hand, let's just look at this hollow cylinder.
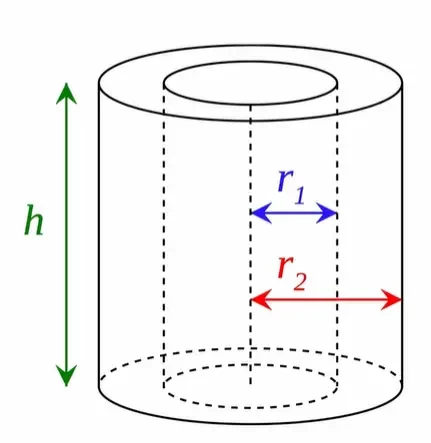
This cylinder have:
Inner radius = r1
Outer radius = r2
Height = h
To get the volume of this figure we can calculate the volume of the cylinder:
$ V_{total} \;=\; V_{Big} \;-\; V_{Small} {2}lt;/p>
$ V_{total} \;=\; π(r_2)^2 h \;-\; π(r_1)^2 h {2}lt;/p>
$ V_{total} \;=\; π [(r_2)^2 \;-\; (r_1)^2 ] h {2}lt;/p>
$ V_{total} \;=\; π [(r_2\;+\;r_1)(r_2\;-\;r_1) ] h {2}lt;/p>
$ V_{total} \;=\; 2π \frac{(r_2\;+\;r_1)}{2} (r_2\;-\;r_1)h {2}lt;/p>
$ V_{total} \;=\; 2π \frac{(r_2\;+\;r_1)}{2} (r_2\;-\;r_1)h {2}lt;/p>
$ V_{total} \;=\; 2πr(r_2\;-\;r_1)h {2}lt;/p>
$ V_{total} \;=\; 2πrΔrh {2}lt;/p>
Getting Volume by Shell Method
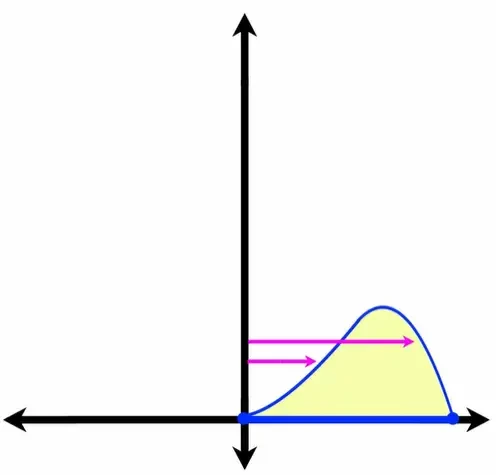
The reason this is useful is that we no longer have to solve for “x” in terms of “y”. If we picture one possible cylindrical shell it will have :
Height = f(x)
Radius = r
Circumference = C = 2πx
So the volume by using the cylindrical shell method will be:
$ \int 2πx [f(x)] \; dx {2}lt;/p>
As we discussed an example for the explanation of the shell method, So according to the above example
f(x) = 2x2-x3
So, let's plug that in for f(x) and then simplify:
$ \int_0^2 2πx (2x^2 - x^3) \; dx {2}lt;/p>
$ 2π \int_0^2 x (2x^2 - x^3) \; dx {2}lt;/p>
$ 2π \int_0^2 (2x^3 - x^4) \; dx {2}lt;/p>
$ 2π \Biggr| \frac{2x^4}{4} - \frac{x^5}{5} \Biggr|_0^2 {2}lt;/p>
$ 2π \Biggr| \frac{x^4}{2} - \frac{x^5}{5} \Biggr|_0^2 {2}lt;/p>
Putting the upper and lower limits in it
$ 2π \left[ (\frac{2^4}{2} - \frac{2^5}{5}) - (0) \right] {2}lt;/p>
$ 2π \left( 8 - \frac{32}{5} \right){2}lt;/p>
$ \implies \frac{16π}{5} {2}lt;/p>
Conclusion
It may have seemed complex because we derived the formula for the volume of the cylinder. We won't have to do that every time we just need to know that the volume of the solid with a cylindrical shell oriented vertically will be equal to:
So we can see that for this particular example this method ended up being easier than the washer method.
For any solid of revolution, you are looking at whether the cross-section is a disc or washer?
You will just have to think critically to figure out which approach is best. Depending on whether it is easy to find the radius or radii of the cross-section with the function or functions as given, or whether it is easier to express things another way.