Using a Definite Integral Calculator
Definite integral calculator is an online calculator that can calculate definite integral eventually helping the users to evaluate integrals online. The integral has 2 major types including definite interals and indefinite integral.
Definite integration calculator calculates definite integrals step by step and show accurate results. Indefinite integration calculator has its own functionality and you can use it to get step by step results also.
If you want to calculate definite integral and indefinite integral at one place, antiderivative calculator with steps is the best option you try.
Related: How to evaluate integrals using partial fraction?
Using our definite integration calculator is very easy as you need to follow these steps:
Step no. 1: Load example or enter function in the main field.
Step no. 2: Choose the variable from x, y and z.
Step no. 3: Give the value of upper bound.
Step no. 4: Give the value of lower bound.
Step no. 5: Verify you equation from the preview whether it is correct.
Step on. 6: Click on the "CALCULATE" button in this integration online calculator.
Formula used by Definite Integrals Calculator
Definite integral calculator uses the below-mentioned formula to show step by step results. If F is the indefinite integral for a function f(x) then the definite integration formula is:
$ \int_a^b f(x) dx = F(b) - F(a) {2}$
How definite integration calculator works?
The definite integral calculator works online to solve any of your equation and show you the actual result along with the steps and graph etc. For calculating the results, it uses the integral rules and formulas accordingly.
You can also solve double definite integration equations by using multiple integral calculator with steps. Similarly, you can also calculate triple definite integration equations using triple integrals calculator with steps.
Evaluating Definite Integrals
Step 1: Understand what a definite intregral actually is
What is a Definite Integral?
A definite integral represents the net area between a function \(f(x)\) and the x-axis over a specified interval \([a, b]\). This takes into account both the area above the x-axis (positive values) and the area below the x-axis (negative values). Similar to an integral calculator but a definitie integral represents a mathematical function vs a calculation.
Example:
When you see the expression \(\int_{0}^{2} x^2 \, dx\), it asks for the net area between the curve \(x^2\) and the x-axis from \(x=0\) to \(x=2\).
Step 2: Identify the Antiderivative
Using the Fundamental Theorem of Calculus, we know that to calculate the net area, we need to find an antiderivative of the function. An antiderivative, \(F(x)\), of a function \(f(x)\) is a function whose derivative is \(f(x)\).
Why this matters
The antiderivative accumulates the values of \(f(x)\). By evaluating the difference between the accumulated values at two points, we effectively calculate the net area between those points.
Example:
For \(f(x) = x^2\), an antiderivative is \(F(x) = \frac{1}{3}x^3\). You can verify this by differentiating \(F(x)\); you should get \(f(x)\) back.
Step 3: Evaluate the Antiderivative at the Upper Limit
We really need antiderivatives for definite integrals. Plug the upper limit of integration, \(b\), into the antiderivative \(F(x)\). This gives you the accumulated value up to the point \(b\).
For \(F(x) = \frac{1}{3}x^3\) and \(b = 2\), \(F(2) = \frac{1}{3}(2^3) = \frac{8}{3}\).
Step 4: Evaluate the Antiderivative at the Lower Limit
Similarly, plug the lower limit of integration, \(a\), into the antiderivative \(F(x)\). This gives the accumulated value up to point \(a\).
For \(a = 0\), \(F(0) = \frac{1}{3}(0^3) = 0\).
Step 5: Subtract to Find the Net Area
Using the results from Steps 3 and 4, subtract the accumulated value at \(a\) from the accumulated value at \(b\):
\[ \text{Net Area} = F(b) - F(a) \]
Example:
\[ \frac{8}{3} - 0 = \frac{8}{3} \]
So, \(\int_{0}^{2} x^2 \, dx = \frac{8}{3}\).
Step 6: Interpret and Verify
Understanding the result contextually can help solidify the concept. It's not just about finding the right answer. It's about understanding the concept and Plotting \(f(x)\) over the interval [a, b] provides a visual representation. The shaded area under the curve corresponds to the value of the definite integral.
Validation:
For functions that are always positive over [a, b], the definite integral should be positive. For functions always negative, the result should be negative. For functions that cross the x-axis, consider the net effect.
Plotting \(x^2\) from 0 to 2, you'd see a parabolic curve above the x-axis. The shaded area beneath it up to the x-axis represents the net area of \(\frac{8}{3}\).
Key Points to Remember:
- Antiderivative's Role: The antiderivative isn't just a mathematical trick; it's intrinsically linked to the concept of accumulation, which is why it's pivotal in evaluating definite integrals.
- Net Area Concept: Definite integrals consider both positive and negative areas. This "netting" is why functions below the x-axis produce negative values for integrals.
- Practice: There’s a vast variety of functions out there. The more you practice, the more intuitive finding antiderivatives and evaluating definite integrals becomes.
Remember, getting to the answer is important, but in my class, showing your work will be the difference between getting credit for the work and just typing on a calculator. It can save a grade, plus also be a way of seeing where you possibly went wrong to correct mistakes.
Also find the unique method of cylindrical shells calculator for calculating volume of shells of revolutions. Disc method calculator with steps for calculating cross section of revolutions. Washer method calculator with steps for calculating volume of solid of revolution.
Frequently Asked Questions
How to evaluate the definite integral?
Definite integrals are defined form of integral that include upper and lower bounds. These integrals can be evaluated by integration and then substitution of their boundary values. Moreover, evaluate the definite integral calculator can also helps to evaluate that type of problems.
When to use u-substitution definite integral?
In definite integrals, u-substitution is used when the function is hard to integrate directly. By u-substitution method, the function can be changed to another by changing variables and the variable of integration.
Ultimately u-substitution is tricky to solve for students in calculus, but definite integral solver makes it easier for all level of calculus scholars.
What Does Area Under the Curve Mean?
An area under the curve means that how much space a curve can occupy above x-axis. The best way to find area under a curve is by definite integral area calculator because there is no specific formula to find area under a curve.









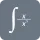
















 Google Play
Google Play
 App Store
App Store

0 Comment