Using Our Indefinite Integral Calculator
Indefinite integral calculator helps you to solve integrals online. With indefinite integrals calculator you can not calculate definite integration. For calculating that you need to use definite antiderivative calculator. If you want to use both definite and indefinite together, use online antiderivative calculator.
Related: Evaluate definite and indefinite integrals using partial fraction?
Indefinite Integral Calculation
Integration is important concept within calculus which students must learn. Online calculators are vital for learning and understanding the difficult concepts because you can try again and again. Similarly, Indefinite integration calculator makes it easy for someone to quickly understand and learn the concept. The different results, along with plot and graphs etc helps someone to learn quickly
Related: Also find step by step washer method calculator and step by step disc method calculator.
How Indefinite integration calculator works?
The indefinite integrals calculator uses the integration formula to solve a specific function online. It uses the integration rules and different other concepts to get accurate results. Definite and indefinite integrals are two main types of integration.
Also find double integration calculator with steps and triple integration calculator with steps on this website for you advance learning and practice regarding multiple integration.
How to find Indefinite Integrals Calculator?
You can search on Google directly to find the indefinite integral calculator. But there will be many suggestions as you need to pick the one who works accurate and fast. You can also find this online indefinite integral calculator within our website.
How to use Indefinite Integral Calculator with steps?
It is very easy to use indefinite integrals calculator with steps. Just follow the mentioned steps:
Step no. 1: Load example or enter function in the main field.
Step no. 2: Choose the variable from x, y and z.
Step no. 3: Verify you equation from the preview whether it is correct.
Step on. 4: Click on the "CALCULATE" button to calculate indefinite integral.
Also find shell method volume calculator which can help you finding the volume of cylindrical shapes.
We hope you liked this indefinite integral solver and the article also helped you to learn how it works. There are many other integration related blogs and calculators such as fourier series calculator with steps and laplace transform calculator with solutions. You can use this calculators for free on this platform and make your learning easy.
Frequently Asked Questions
How to find the indefinite integral?
An indefinite integral is a type of integral which does not have upper and lower bound. These integral can be solved by integrating a given function. For example, the solution of an indefinite integral ∫ cos(x) dx is,
$ \int cos(x) dx \;=\; sin(x)+c {2}{2}$
You can find the indefinite integral calculator to get accurate results online.
How to represent indefinite integral?
Indefinite integral is a function that contains derivative of a function without its boundaries. To represent them, we simply use integration sign and the variable of integration such that,
$ \int f(x) dx {2}{2}$
To solve this type of integral, indefinite calculator is one of the best option.
How do you difference definite vs indefinite integral?
You can easily differentiate both integrals according to their specific properties. Definite integrals are defined by using upper and lower bound of a function. On the other hand, indefinite integrals are defined without any upper and lower bound.For this purpose, evaluate indefinite integral calculator is the best option.
Evaluate the indefinite integral as an infinite series.∫( (cos(x)-1 )⁄x ) dx
Since the given integral is indefinite so we are going to use Maclaurin series to express it.
$ cos(x) \;=\; \sum_{n=0}^∞ \frac{(-1)^n x^{2n}}{(2n)!} {2}{2}$
And,
$ cos(x) - 1 \;=\; \sum_{n=0}^∞ \frac{(-1)^n x^{2n}}{(2n)!} - 1 {2}{2}$
Since n = 0 gives 1, So
$ cos(x) - 1 \;=\; \sum_{n=1}^∞ \frac{(-1)^n x^{2n}}{(2n)!} {2}{2}$
Simplifying,
$ \frac{cos(x) - 1}{x} \;=\; \sum_{n=1}^∞ \frac{1}{x} \frac{(-1)^n x^{2n}}{(2n)!} $ $ \frac{cos(x) - 1}{x} \;=\; \sum_{n=1}^∞ \frac{1}{x} \frac{(-1)^n x^{2n-1}}{(2n)!} {2}{2}$
On the other hand, use to evaluate the indefinite integral calculator for solving the integral without upper and lower limits values.









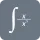








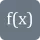

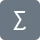







 Google Play
Google Play
 App Store
App Store

0 Comment