Introduction to Area between Curves Calculator
The area enclosed by the two curves calculator is an online tool to calculate the area between two curves. Using limits, it uses definite integrals to calculate the area bounded by two curves. It provides you with a quick way to do calculations rather than doing them manually.
In calculus, the area under a curve is defined by the integrals. Similarly, the area bounded by two curves can be calculated by using integrals. We introduce an online tool to help you find the area under two curves quickly. This tool can save you the time and energy you spend doing manual calculations.
How to find the area between two curves calculator with steps?
The area between curves calculator with steps is an advanced maths calculator that uses the concept of integration in the backend. You can easily find this tool online. For this, follow the given steps;
- Use the main keyword to search for the tool from your desired browser.
- Your search engine will provide you with different results. Choose the area between two curves calculator from these results.
- On the website page, there will be a list of integral tools.
- Select the desired tool from the list. Or you can also use our different tools, such as the area under graph calculator.
Formula used by Region Bounded by Curves Calculator
The area between two curves is one of the major concepts of calculus. It is defined as the space enclosed by two curves between two points. The difference of integral between two functions is used to calculate area under two curves. For example, the first curve is defined by f(x) and the second one is defined by g(x). So, the total area between f(x) and g(x) on the interval (a,b) is:
$A=\int^b_a[f(x)-g(x)]dx{2}$
Where,
- f(x) and g(x) are two curves.
- ∫ba is the integral symbol.
- dx is the coefficient of integral.
The above formula is used by the area between 2 curves calculator to provide you a quick and easy solution.
How to use area bounded by curves calculator?
It is effortless to compute calculations by using this tool. Only you have to follow the given steps. These steps will help you to find the area bounded by two curves in a step-by-step way.
- Enter the function of the first and second curves in the input box. This step is to enter the input functions.
- Select from the menu definite or indefinite integral. If the area is bounded between two points, choose a definite integral. Otherwise, you can use indefinite integral.
- In the case of definite integral, write the value of the upper and lower bound.
- Now choose the variable of integration, i.e., x, y, or z.
- Review the input value and click the calculate button.
After clicking the calculate button, the area between the curves calculator and steps will provide quick results.
Why to use Area Enclosed by two Curves Calculator?
Integration and differentiation are two significant concepts in calculus. The area bounded by curves calculator is the best online tool for easy step-by-step calculation. It is reliable for both mathematicians and students and assists them in solving real-life problems.
The main reason to use this tool is to give you easy and fast calculations. While using this online tool, you can also get a visual interpretation of the given integral. It also provides you with all possible intermediate steps along with the graph of integral. Therefore, it would be best to use this tool.
Benefits of using Area between 4 Curves Calculator
Finding the area bounded by two curves is a long and tricky procedure. Therefore, using an online tool can help get easy solutions. All you need to have good internet and some click for it. The use of this online calculator will provide you following benefits:
- It saves time by providing you area under two curves within a few seconds.
- It has a user-friendly interface so that you can use it easily.
- It provides you with all possible intermediate steps, visual representation, Riemann Sum, and definite and indefinite integrals with just a few clicks.
- It allows you to practice with different examples.
- It is a free online calculator, so you don’t need to pay.
We hope you enjoy using the most advanced and demanded integrals tool. Numerous tools are also available in the integral calculator to help you integrate. You can also use convergent or divergent calculator to learn integrals easily.
FAQ's
How to find the area of a region between two curves?
The area of a region between two curves can be calculated by using definite integrals. For this, you have to integrate the difference of both functions and then substitute the values of upper and lower bounds. The formula to calculate area between two curves is:
$A= \int^b_a [f(x)-g(x)]dx{2}$
What is an integral area?
The integral area is the sum of areas of infinitesimal small portions in which a shape or a curve is divided. It can be calculated by using definite and indefinite integrals.
What is the rule of calculating area?
The area is the measure of total space inside a surface or a shape. To calculate the area of a rectangle or a square, multiply the width and height. And the area under a curve can be calculated by finding the area of all small portions and adding them together.









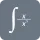








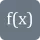

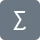







 Google Play
Google Play
 App Store
App Store

0 Comment