Introduction to Laplace Transform Calculator

You can use an online Laplace transformation calculator with steps for the conversion of a real-valued function to a complex-valued function. In engineering and research, the laplace transformation is used to analyze control systems and electronic devices.

The laplace calculator can also be used to solve differential equations using the Laplace transform equation. Continue reading to learn more about Laplace transforms and laplace integral calculator.

Related: This website helps you learn the calculations regarding double and triple integrals. You can find multivariable integral calculator and volume integral calculator for accurate calculations of double integrals and triple integrals.

What is Laplace Transform?

Laplace transformations describe integral transformations in calculus that convert a real-valued function f (t) to a complex-valued function. This transformation is used to convert normal differential equations into algebraic equations that may be used to solve ordinary differential problems.

A linear differential equation is quite common in practical uses, and it frequently emerges from electrical engineering, physics, and control systems challenges. Apart from that, the laplace calculator with steps can only perform regular Laplace transforms, also known as unilateral laplace transforms.

This is because only one side of the Laplace transform (the ordinary side) is used and the inverse Laplace transform side is not used. An integral calculator by parts, on the other hand, can be used to calculate the integrals of functions concerning variables in concern.

Related: You can also find indefinite integral calculator and definite integral calculator to find definite integral online.

Formula used by Laplace Calculator

The laplace transform integral calculator uses below formula to calculate and provide accurate results.

$ F(s) \;=\; \int_0^{+∞} f(t) \;.\; e^{-st} \;.\; dt {2}$

How Laplace Transformation Calculator works?

The inverse laplace transform calculator works online. It requires input from user and by its transformation method, you can turn actual functions into complex functions. The laplace calculator calculates the results quickly in the form of steps, plots, graphs etc.

There are useful other calculators which you can use on this website like cylindrical shell calculator and washer integral calculator for washer method.

How to use Laplace Integral Calculator?

It is very easy to use laplace transform calculator with steps. You just need to follow belowmentioned steps to get accurate results.

Step 1: In the input field, type the function, function variable, and transformation variable.

Step 2: Click on to "Load Example" to calculate any other example (Optional).

Step 3: To acquire the integral transformation, click the "Calculate" button.

The laplace calculator will shows the results as:

• First and foremost, the laplace transform calculator with step by step solution displays your input as an ordinary differential equation.
• Then, in algebraic form, it displays the answer to the equation.
• It also shows plots of given algebraic functions.

Also find other online integration tools on this website like the disc calculator and fourier sine transform calculator will help you a lot regarding your calculations online.

How to solve a question with Laplace Calculator?

For solving this, you'll have to provide the values of your function in the input of the laplace transform calculator step by step.

The Input is

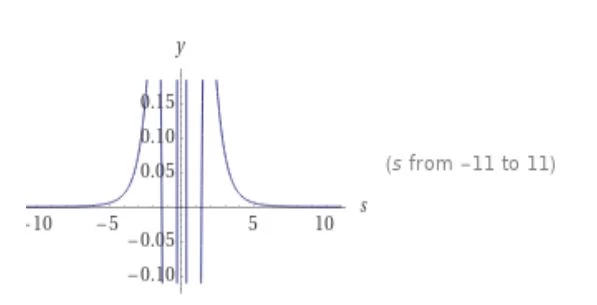
$ L_t \left[ t^4 \; sin(t) \right] (s) {2}$

Result:

$ \frac{24 (5s^4 - 10s^2 + 1)} {(s^2 + 1)^5} {2}$

Plot

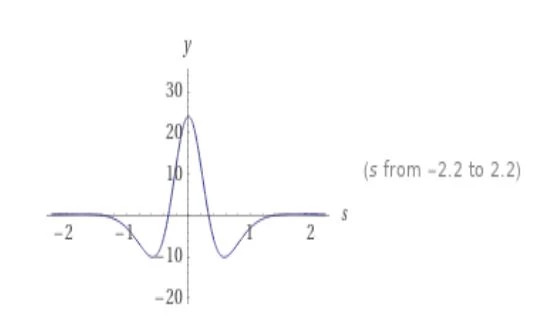
Plots

There are useful blogs on this website which you can find helpful. Click on to learn more about integral of fraction and the importance of integral calculus.

Conclusion

Try this laplace transform calculator with steps to see how a real ordinary differential equation is transformed into a complex algebraic expression. You can certainly perform all of these calculations properly, but it is a difficult and time-consuming operation. As a result, students and professionals can quickly calculate using this laplace transformation calculator.

Related: Also learn how to integrate using calculator and how easy it is to understand which method to use for finding volume of solid of revolutions.

Other useful tools

• finding area between curves calculator
• simpson's rule formula calculator
• arc length integration calculator
• arc length of polar curves calculator
• imit of sum calculator with steps

Frequently Asked Questions

What is the Laplace Transform's principal purpose?

The Laplace Transform is used to solve differential equations. The Laplace transform's principal purpose is to convert Ordinary Differential Equations (ODEs) into algebraic variables. This conversion aids in the simple solution of ODEs.

The process of converting ordinary differential equations into the algebric variable is tricky due to long manual calculations. But the laplace transform calculator step by step make it quite easier for students of any level.

Can we solve differential equation using laplace transform calculator?

Yes, this laplace differential equation calculator helps you calculate your query and it provides you with steps and graph.

What are the Most Common Laplace Transform Uses?

The following are some of the most common uses of the Laplace transform with steps. These benefits of Laplace transformation is also available in laplace transform calculator with step by step solution:

• It is used to solve differential equations.
• It is used in many areas of Physics such as to derive the circuit.
• It is used in Integrated Circuit.
• It is used in control systems to mentain load frequency.

What is the distinction between the Fourier and the Laplace Transforms?

The Fourier transform alters the magnitudes of a signal by decomposing a function that is location or time-dependent.

Laplace transform, on the other hand, modifies the magnitude and oscillation portions which can calculate by using laplace transform calculator with steps free. The main set of the Fourier Transform is the Laplace Transform.

What Is the Laplace Transform and Why Is It Important?

When basic conditions are given, such as zero initial numbers, the Laplace transform can be used to find specific forms of differential problems.

We hope this laplace transform calculator with solutions helped you in your work. This Laplace inverse calculator is made solely for your help so your appreciation would be a lot to us.