Introduction to Fourier Transform Calculator
The fourier transform calculator with steps is an online tool which helps you to find fourier transformation of a specified periodic function. The fourier transform solver allows you to transform a function of time into function of frequency.
What is the Fourier Transform?
The Fourier Transform is a mathematical term that describes the expansion of a periodic function as follows of infinite summation of sine and cosines. With the assistance of a fourier transformation calculator, you can determine the results of transformation of functions and their plots.
To calculate Laplace transform method to convert function of a real variable to a complex one before fourier transform, use our inverse laplace transform calculator with steps.
Fourier transform of odd and even functions: The fourier coefficients a 0, a n, or b n may get to be zero after integration in certain Fourier transform problems. It indicates that attempting to discover the zero coefficients could be a lengthy operation that should be avoided. However, if we have a good understanding of odd and even functions, we can estimate the zero coefficients easily before we begin integration.
Related: Find what are cruicial methods to find volume of solid revolutions.
Addition Properties
When two even functions are added together, the result is always an even function.
The difference between two odd values is also odd.
The product of odd and an even value is neither even nor odd (unless one of the functions is equal to zero)
Related: Double integration and triple integration also belong to crucial ones in the world of integration. You can use a multiple integration calculator and triple integral online calculator to calculate double and triple integrands online.
Properties of Multiplication
When two odd functions are multiplied together, the result is always even.
When two even functions are multiplied, the result is also even.
A fourier transformation calculator transforms and generate result with plots.
Related: 5 Benefits of using Integration Calculator as well as integration by u substitution calculator.
What Is a Fourier transformation Calculator and How Does It Work?
The online fourier transform calculator can assist you in finding precise results whenever you encounter complex functions. Using this fourier transform tool, you will receive a proper scenario of the computations. It will make your calculus and math learning easier!
Input:
- Take a look at what you've required to do.
- First, select your function.
- Click on the 'calculate' button.
Output:
- At first it shows the input function as it is.
- Then it calculates the Fourier transformation of that function.
- It also includes a plot section where plots are displayed according to the imaginary and real part.
This calculating method is one of the simplest methods to calculate integrands easily. You can calculate the volume of a slice of a solid with a disk washer calculator. Fourier transform calculator is overall very simple and easy to use.
Solved Example:
Find Fourier transformation of:
$F_t\;[e^{-t^2} sin(t)]\;(w){2}lt;/p>
Solution:
Input function:
$F_t\;[e^{-t^2} sin (t)]\;(w){2}lt;/p>
Transformed Results:
$\frac{1}{\sqrt2π}\;\int_{-∞}^∞\left(e^{-t^2} sin(t)\right)e^{iwt} dt\;=\;-\frac{1}{2}\mathcal i\;\left(\frac{e^{-\frac{1}{4}(w+1)^2}}{\sqrt 2}\;-\;\frac{e^{-\frac{1}{4}(w-1)^2}}{\sqrt 2}\right){2}lt;/p>
Plots:
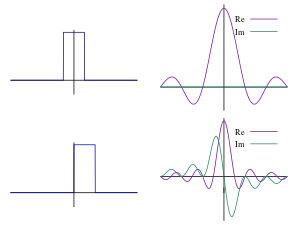
Related: Understanding Integration by Partial Fraction in 5 Minutes!
Other useful tools
- total area between curves calculator
- simpson's rule integral calculator
- arc length formula integral calculator
- length of polar curve calculator
- summation limit calculator
Conclusion
Fourier transformation has a wide range of applications in engineering and technology because they are important in signal processing, acoustics, shell theory, quantum physics, and image processing, all of which make greater use of fourier calculator. Furthermore, the crucial benefit of Fourier analysis is that it protects minimal information throughout the signal processing procedure.
Related: Learn more about integral washer method and find how useful is cylindrical shells volume calculator for volume of solid revolutions.
FAQ’s:
Is there anything special about the Fourier series?
The Fourier series is always unique, regardless of the number n. You can use fourier series calculator step by step for learning and practice.
Where is Fourier transformation used?
The orthogonality relationship between sine and cosines is utilized by the Fourier transformation.
Is there a Fourier transformation in all functions?
The fourier transform refers to any periodic function that is defined across the complete real line. Our fourier sine transform calculator, on the other hand, can help you determine whether a function has Fourier transformation.
Related: There are many other online calculators which provide easy step by step solutions related to different integration methods and types. Such as to calculate definite integration and indefinite integration you can use our definite integral calculator and indefinite integral online calculator for free.
Give a key reason why the Fourier transformation should be used?
The fourier transformation key advantage is that it allows us to quickly study a signal in a domain beyond its original.
Is the inverse Fourier transform linear?
Yes, the inverse Fourier transform is also linear just like Fourier transform. Consider the inverse Fourier transformation and Fourier transformation for f(x).
$ f(x) \;=\; \int_{−∞}^∞ \; F(k) e^{2πikx} dk {2}lt;/p>
And,
$ F(k) \;=\; \int_{−∞}^∞ \; f(x) e^{2πikx} dx {2}lt;/p>
Since the Fourier transformation is linear, by using same augment we can show the linearity of inverse Fourier transform for F(k) and G(k).
$ aF(k) \;+\; bG(k) \;=\; \int_{−∞}^∞ \; [af(x) \;+\; bg(x)] \; e^{−2πikx} dx {2}lt;/p>
Or
$ aF(k) \;+\; bG(k) \;=\; a \; \int_{−∞}^∞ \; f(x) \; e^{−2πikx} dx \;+\; b \int_{−∞}^∞ \; g(x) \; e^{−2πikx} \; dx {2}lt;/p>
Furthermore, you can use inverse fourier transform calculator to calculate your equations easily online.
What is the Fourier sine transform of 1/x?
We have Fourier sine transformation of f(x), such that,
$ F[f(x)] \;=\; \int_0^∞ f(x) \; sinsx \;dx \;=\; F(s) {2}lt;/p>
Now, for f(x)= 1/x
$ F[f(x)] \;=\; \int_0^∞ \frac{1}{x} sinsx \; dx {2}lt;/p>
Let
$ sx \;=\; y \implies x \;=\; \frac{y}{s} \implies dx \;=\; \frac{dy}{s} {2}lt;/p>
Now,
$ f(x) \;=\; \int_0^∞ \frac{sin y} {y} dy \;=\; \frac{π}{2} {2}lt;/p>
You can use fourier sine transform calculator to get instant and accurate results online.
When to use Fourier sine and cosine transform?
There are two conditions to check whether the Fourier sin or cosine is helpful.
- When the given function is odd, i.e. f(−x)=−f(x), we use sine transformation.
- But when the function is even, i.e. f(−x)=f(x), we can use cosine transformation.
Our fourier cosine transform calculator provide step by step results so you can learn and practice online.
Is Fourier transformation exponential?
There are two types of Fourier transformation that are trigonometric series and exponential series. The exponential Fourier transformation represents periodic function that is referred to exponential function. So, it is just another type of Fourier transformation. Use fourier transform tool and learn through its graph, steps and chart.
we hope you liked our fourier integral calculator. You can also use integration by parts calculator with steps free on the home page of this website.



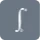
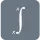






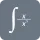
















 Google Play
Google Play
 App Store
App Store

0 Comment