Introduction

We can find the volume obtained by rotation by using the concept of indefinite integral. The volume of solid revolution is obtained from an indefinite integral if it revolve around a plane region. But for this to happen, the line must not pass through that plane. So there are three methods to do this type of revolution around a vertical or a horizontal line. These methods are:

1. Disk Method
2. Washer Method
3. Shell Method

In this article we will explain different methods used for finding volume of solid revolutions and the difference between three of them. This will make you understand when to use each these methods.

Related: Learn about different types of integration methods and how to understand integration of partial fraction quickly.

How to determine which Method to Use for Volume?

If you want to determine which method to use for volume of solid revolutions, it depends on the type of rotation evolving in it. The below flowchart help you to analyze which method is to use:

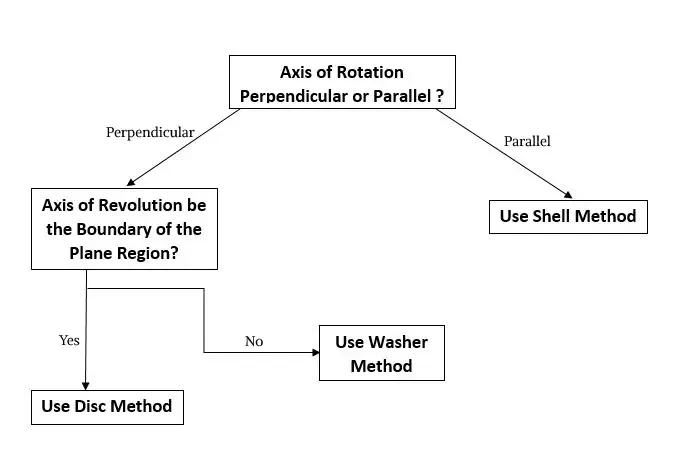
Now this raises a question, Is the axis of revolution parallel or perpendicular?

Best way to deal with this is that if it's parallel, we can use shell method to find the volume.

But in case if it is perpendicular, it raises another question. Does the axis of revolution is on the boundary of the plane region?

If axis of rotation is at boundary of the plane we should use the disk method to find the volume of solid revolution and if axis of rotation is not at boundary of the plane then use should use washer method to find the volume of solid of revolution.

Now one more question arise that which method is best fit in our problems. So before we go through qurstion problems we may concern when to use washer or shell method for finding volume.

These questions makes it easy for someone to understand which method is fit to use. Now, let's find the difference between these methods.

Related: What are the benefits of using integral calculator?

Disk Method

The disk method is the method for calculating the volume of solid-state material which revolve around the axis. This may be along the x-axis or y-axis depending on the requirement.

Disc method is used where the axis of rotation is attached with the boundary of the plane region. It becomes easy to calculate the volume of a solid around a line or its axis of rotation by using disc method.

In the Disk method Integration, if we create a three-dimensional shape of a solid region obtained by the revolution of our function. And divide it into an infinite number of discs of different radius having infinitesimal thicknesses, we will be able to find the volume of each disc with a different radius.

You can also use integration by parts calculator with steps on home page of this integral website.

Rotation along X-axis

If the function to be revolved is along the x-axis, then integral represents the volume of the solid of revolution:

$ V \;=\; \int_a^b (π R^2) (w) {2}lt;/p>

$ \text{Or, } V \;=\; \int_a^b π f(x)^2 \; (Δx) {2}lt;/p>

$ V \;=\; \int_a^b π f(x)^2 \; dx{2}lt;/p>

Rotation along Y-axis

If the function to be revolved is along the y-axis, then integral represents the volume of the solid of revolution:

$ V \;=\; \int_a^b (π R^2) (w) {2}lt;/p>

$ \text{Or, } V \;=\; \int_a^b π f(y)^2 \; (Δy) {2}lt;/p>

$ V \;=\; \int_a^b π f(y)^2 \; dy{2}lt;/p>

Here f(x) and f(y) show the radii of the disks we have created in solid three dimensional shape or the distance between the axis of revolution and a point on the curve.

Now we will understand this concept in a practical way with detailed example

Example

Let's find the volume of the solid obtained by rotating the region under the graph y = x 2 about the x-axis over the interval of [−2,3].

Solution:

Since the x-axis is the boundary point of the region. So disc method is used here and the graph of such function for obtaining solid region is given as:

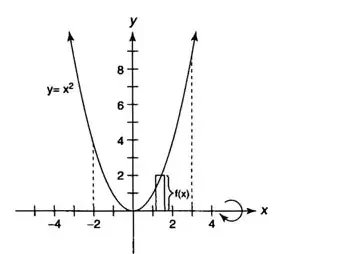
The volume of a solid revolution by disk method is calculated as:

$ V \;=\; \int_{-2}^3 π (x^2)^2 dx {2}lt;/p>

$ V \;=\; π \int_{-2}^3 x^4 dx {2}lt;/p>

$ V \;=\; π \left[ \frac{1}{5}x^5 \right]_{-2}^3 {2}lt;/p>

$ V \;=\; π \left[ \frac{243}{5} \;-\; \left( \frac{-32}{5} \right) \right] {2}lt;/p>

$ V \;=\; 55π {2}lt;/p>

You can also use disk method calculator to learn while doing doing practice online.

Washer Method

Washer method is an integrating method for finding the volume of a solid in which the axis of rotation is not attached with the boundary of the plane and cross-section are taken perpendicular to the axis of rotation.

Washer method for finding the volume is also known as the ring method because we will have to see the disk with a hole in it or we can say there is a disk with a disk removed from its center.

There is a shape of the slice obtained in a graph of the washer method from which we generate a disk with a hole in it, so we subtract the area of the inner circle from the area of the outer circle. Thus if R is the radius for outer of the disk and r is the radius for inner of the disk, then area will be calculated as:

πR² – πr²

For the volume of function, we will multiply the area with the thickness of the disk. The volume will be calculated both in terms of x-axis and y-axis depending upon the problem. You can also use washer integral calculator for calculating it online.

Rotation along X-axis

The volume(V) of the solid generated by rotating the curve between f(x) and g(x) on an interval of [a,b] about the x-axis is given as:

$ V \;=\; \int_a^b π \left( [f(x)]^2 \;-\; [g(x)]^2 \right) dx{2}lt;/p>

Rotation along y-axis

Similarly, the volume(V) of the solid generated by rotating the curve between f(x) and g(x) on an interval of [a,b] about the y-axis is given as:

$ V \;=\; \int_a^b π \left( [f(y)]^2 \;-\; [g(y)]^2 \right) dy{2}lt;/p>

Here, f(x),g(x),f(y) and g(y) represent the outer radii and inner radii of the washer volume.

Now we will understand in a practical way with a detailed example

Example

Let's find the volume of the solid generated by rotating the curve between y = x²+2 and y = x+4 about the x-axis.

Solution:

Since, y = x²+2 and y = x+4, So

x²+2 = x+4

x²-x-2 = 0

(x+1)(x-2) = 0

x = -1 and x = 2

From that, the graph of the above functions will intersect at (-1,3) and (2,6), It will be given as:

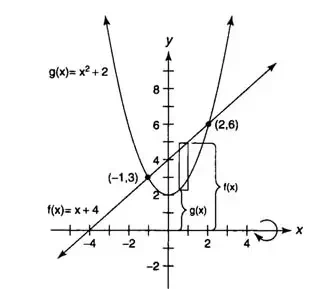
The volume of a solid revolution by washer method is calculated as:

$ V \;=\; \int_{-1}^2 π \left[ (x+4)^2 - (x^2 + 2)^2 \right] dx {2}lt;/p>

$ V \;=\; \int_{-1}^2 π \left[ (x^2 + 8x + 16) - (x^4 + 4x^2 + 4) \right] dx {2}lt;/p>

$ V \;=\; π \int_{-1}^2 (-x^4 - 3x^2 + 8x + 12) dx {2}lt;/p>

$ V \;=\; π \left[ -\frac{1}{5} x^5 - x^3 + 4x^2 + 12x) \right]_{-1}^{2} {2}lt;/p>

$ V \;=\; π \left[ \frac{128}{5} - \left( - \frac{34}{5} \right) \right] {2}lt;/p>

$ V \;=\; \frac{162}{5} π {2}lt;/p>

Also find useful other online calculators like double integral calculator polar and triple integration by parts online. These online calculators can help you a lot in learning double and triple integration.

Shell Method

Shell method is a contrast method to the disc/washer method to find the volume of a solid. In the shell method, cross-sections of the solid are taken parallel to the axis of revolution.

If the cylindrical shell has a radius r and height h, then its area will be 2πrh. Thus the volume by shell method is 2πrh times its thickness. You can use volume by shell method calculator for calculating any equation of shell method.

The volume in terms of x-axis and y-axis will be calculated in different ways which are given below

Rotation along x-axis

The Volume(V) of the solid is obtained by rotating the region y = f(x) when rotated about the x-axis on the interval of [a,b], then the volume is:

$ V \;=\; \int_a^b 2πx \; f(x) \; dx {2}lt;/p>

Rotation along y-axis

The Volume(V) of the solid is obtained by rotating the region x = f(y) when rotated about the y-axis on the interval of [a,b], then the volume is:

$ V \;=\; \int_a^b 2πy \; f(y) \; dy {2}lt;/p>

Here the x and y under the integral (integrand) are the radii of the shell method, while on the other hand f(x) and f(y) represent the height of the shell method.

Let’s move on to an example for a better understanding of the Shell method to find the volume of solid.

This website help you solve indefinite integral online and definite integral online by using online calculators.

Example

Find the volume of solid obtained by rotating the region bounded by y = x2 and x-axis[1,3] when rotated about the y-axis.

Solution:

Since axis of rotation is vertical in shell method, so it will be expressed in terms of x i.e radius of shell is “x” and height of the shell is “f(x) = x^2” as given in a figure:

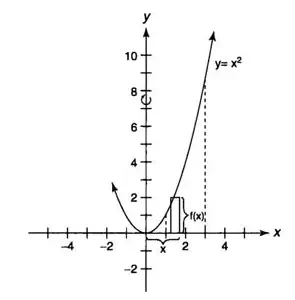
The volume of a solid revolution by cylindrical shell method is calculated as:

$ V \;=\; \int_1^3 2πx \; x^2 dx {2}lt;/p>

$ V \;=\; 2π \int_1^3 x^3 dx {2}lt;/p>

$ V \;=\; 2π \left[ \frac{1}{4}x^4 \right] {2}lt;/p>

$ V \;=\; \frac{π}{2} (81-1) {2}lt;/p>

$ V \;=\; 40π {2}lt;/p>

We hope you liked this article. This website offer a lot of other integration related calculators like laplace transform calculator with steps and fourier series transform calculator which you can use for free.