The washer method and the shell method are powerful methods for finding the volumes of solids of revolution. By making slight modifications to these methods, we can find volumes of solids of revolution resulting from revolving regions.
The revolving regions can be in the XY plane on a vertical line in the y-axis or it can be on the horizontal line in the x-axis.
In this article we will walk through an example to illustrate a shell method and washer method in one such scenario but before we do this let's review the shell method and the washer method.
Shell Method
Suppose that we have a region R, bounded between the curves y=f(x) and y=g(x) from x = a to x = b as shown in a figure.
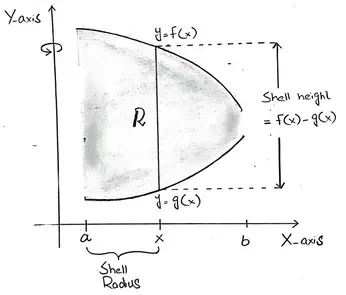
If we take this region and revolve it around the y axis, we obtain the following solid of revolution with a hole in its centre.

For a given value of x in between a and b, if we take the corresponding line segment extending from the curve g(x) to the curve f(x) and revolve this line segment about the y-axis, we obtain the surface of a cylindrical shell.
The height of this shell which is given in the first figure is equal to f(x) - g(x) and the radius of this shell is equal to the value of x.
Recall that the shell method says that the volume of the solid is equal to the integral from[a,b] of 2πx times f(x) - g(x).
Mathematically,
$ Volume \;=\; \int_a^b 2πx \left( f(x) \;-\; g(x) \right) dx $
Here,
x = Shell Radius and
f(x) - g(x) = Shell Height
But keep in mind if we revolve a region R around another vertical line beside the y-axis, the shell radius and the shell height formulas may need to be revised.
Therefore we will need to modify the formula if we revolve R around another vertical line.
Washer Method
For understanding the washer method, we will recall the washer method about the y-axis. Suppose that we have a region bounded between the curves x= Q(y) and x = P(y).
If we revolve this region around the y-axis, then we obtain the following solid that's bounded between the outer surface and the inner surface.

For any value of y in between x = a and x = b. Let's draw a line segment from Q(y) to P(y). If we revolve this line segment about the y-axis, we obtain the surface of a washer-like disk with a hole in it.
Recall that the washer method says that volume is equal to the integral from [a,b] of pi times P(y)2 - P(y)2.
Mathematically,
$ Volume \;=\; \int_a^b π \left( p(y)^2 \;-\; q(y)^2 \right) dy $
Here.
P(y) = radius of the outer circular boundary
Q(y) = radius of the inner circular boundary
Again we will need to modify this formula if we revolve R around another vertical line beside the y-axis.
To illustrate how we can modify the washer method in the shell method in cases where we revolve the region R around a vertical line other than the y-axis.
Let's walk through the following examples.
How to modify Washer Method in Shell Method
Let R be the region bounded in the first quadrant by the curve y = 1-√x, on the x-axis and the y-axis. We want to determine the volume of the solid generated when r is revolved about the line x = -¼.
Solution By Shell Method
The graph of the region R that's bounded by the x-axis the y-axis and the curve y = 1-√x is given below:
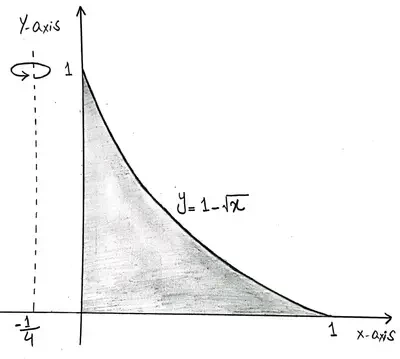
Now suppose we revolve this region around the vertical line x = - ¼. When we do this we obtain the following solid that's bounded in between the surface and the inner cylinder.

For a given value of x in between x = 0 and x = 1 draw a vertical line segment from the x-axis to the curve y = 1-√x, which represents the height of the corresponding cylindrical shell.
Using the shell method the volume is equal to the integral from [0,1] of 2π times the shell radius times the shell height.
$ V \;=\; \int_0^1 2π (Shell Radius)(Shell Height)dx $
$ V \;=\; \int_0^1 2π (x+ \frac{1}{4})(1-√x)dx $
In this case,
Shell Radius = x+¼
Shell Height = 1-√x
Therefore, The volume will be equal to :
$ V \;=\; \int_0^1 2π \left( x+ \frac{1}{4} \right) \left( 1-√x \right)dx $
$ V \;=\; 2π \int_0^1 \left( x - x^{\frac{3}{4}} - \frac{1}{4}x^{\frac{1}{2}} + \frac{1}{4} \right)dx $
$ 2π \left( \frac{1}{2}x^2 - \frac{2}{5}x^{\frac{5}{2}} - \frac{1}{6}x^{\frac{3}{2}} + \frac{1}{4}x \right) \Biggr|_0^1 $
$ \implies 2π (\frac{11}{60}) $ $ \frac{11π}{30} $
Thus, this is the volume otained for the given function by using the shell method. For reducing brainstorming and complex calculations we may also try volume shell method calculator.
Solution By Washer Method
Now let's go back and confirm this result by finding the volume of the solid using the washer method. So once again we are taking the region R and revolving it around the line x = -¼.
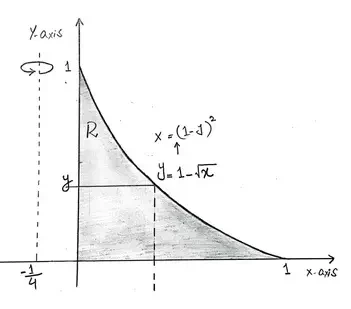
Using the washer method, we pick a value of y in between y = 0 and y = 1, we draw a horizontal line segment through the region R revolving this line segment around the line x = -¼ gives us this surface of a washer.
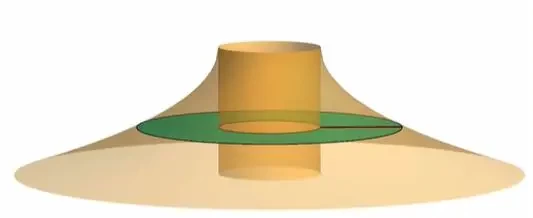
So the volume by washer method is:
$ V \;=\; \int_0^1 π \left( (Outer Radius)^2 - (Inner Radius)^2 \right) $
In this case,
Inner Radius = ¼
Outer Radius = (1-y)2
Therefore, The volume will be equal to :
$ V \;=\; \int_0^1 π \left( \bigr[(1-y)^2 + \frac{1}{4} \bigr]^2 - \bigr[ \frac{1}{4}^2 \bigr]^2 \right) dy $
$ V \;=\; π \int_0^1 \left( y^4 - 4y^3 + \frac{13}{2}y^2 - 5y + \frac{3}{2} \right) dy$
$ V \;=\; π \left( \frac{1}{5}y^5 - y^4 + \frac{13}{6}y^3 - \frac{5}{2}y^2 + \frac{3}{2}y \right) $
$ \implies V \;=\; \frac{11π}{30} $
which equals the value we obtained using the shell method. So now we can say that we can modify the shell method to the washer method.
Volume by solid of revolution is somehow tricky techniques to do. So we can also try the online tools like washer method formula calculator and also volume of a disc calculator because the disc method is also the one of the valueable method for finding the volume of solid of revolution.
Conclusion
As we know the washer method and shell method both apply in the calculations. But the uses of both methods are vital and beneficial method of integration. Sometimes, it is best to use the washer method in case of finding volume of solid revolutions and sometimes the shell method works more efficiently. Either way, both methods are very useful and widely used in finding the volume of solid revolutions. We hope you liked this article, do find other articles in the blog section.