Introduction to the Stoke’s Theorem

In calculus, Stoke’s theorem is a fundamental theorem that generates a relation between a flux of a vector field of a closed surface and the surface integral of the closed surface. It provides a bridge connection between calculus and geometry by providing a relation between the line and surface integral. Let’s understand more about Stoke’s Theorem, statement, proof, and its applications.

Understanding of the Stoke’s Theorem

It is a fundamental theorem of vector calculus that involves the study of the relation between a line integral of a closed surface and the surface integral of the curl of a vector field enclosing the surface. Stoke's theorem is also known as the generalization of Green's theorem in three dimensions. But it is necessary to understand the concept of line integral, surface integral, and curl before understanding Stoke’s theorem. Let’s understand them one by one.

Line Integral

When a function is integrated along a curve, the integral is known as a line integral. We can integrate a vector-valued or a scalar function by using the line integral. Mathematically, the line integral formula can be written as;

$\int_C f(r) ds= \inte^b_a f[r(t)] r’(t) dt$

Surface Integral 

It is a double integral of the line integral which is used to calculate flux across the surface. In other words, the surface integral is the generalization of the sum of multiple integrals over the surfaces. Mathematically, the formula of the surface integral is written as:

$\int \int_S f(x,y,z) dS=\int \int_D f(\vec{r}(u,v))||\vec{r}_u\times \vec{r}_v||dA$

Curl

In vector calculus, the curl is a mathematical operator which is applied to a vector field. It describes infinitesimal circulations of a vector field in three-dimensional Euclidean space. In other words, it is a vector product between the gradient and the vector. The curl of a vector field F is represented by a symbol “∇” which is pronounced as “nabla”. Mathematically, 

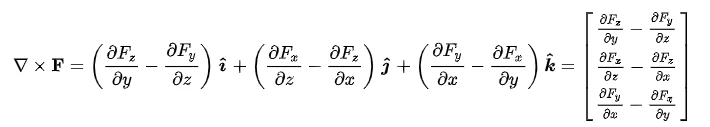
Where, 

• F=[F_x. F_y, F_z] is the vector field.
• ∇ is the gradient vector.

Stoke’s Theorem Statement

According to the statement of Stoke’s theorem,

If S is any surface bounded by a closed curve C and F is the field containing the surface S then, the line integral of a vector field F of a closed curve is equal to the surface integral of the curl of the vector field F taken over the surface S. Mathematically, 

$∮_C \vec{F}. \vec{dr} = \int \int_S (\nabla \times \vec{F}).\vec{dS}$

Where, 

•  C is the closed curve
• S is the surface bounded by the curve C.
• ∇ x F is the curl of the vector field.

Stoke’s Theorem Proof

To prove Stoke’s theorem, we start by assuming the C has a smooth parametrization r=r(s,t), such that curve C corresponds to the region R in the st-plane and S corresponds to the boundary of R. Also assume that F be the vector field around S. 

The line integral around the curve C is, 

$\int_C \vec{F}.\vec{dr}=\int_C \vec{F}.\frac{\partial r}{\partial s}ds+\frac{\partial r}{\partial t}dt$

Suppose that we define a vector field G on the st-plane such that,

$\vec{G}=(G_1, G_2)$

Then, assume that

$\vec{G_1}=\vec{F}.\frac{\partial r}{\partial s}$

And,

$\vec{G_2}=\vec{F}.\frac{\partial r}{\partial t}$

By using this substitution method, we can write the line integral as;

$\int_C \vec{F}.\vec{dr} =\int_C \vec{G}.\vec{ds}$

Now defining the curl of the vector field in terms of parametrization, 

$\int_S \nabla\times \vec{F} \vec{dA}=\int_R (\frac{\partial G_2}{\partial t}-\frac{\partial G_1}{\partial t})ds dt$

Also, by the above substitutions, 

$\int_C \vec{F}.\vec{dr} =\int_C \vec{G}.\vec{ds}$

Hence, we get

$∮_C \vec{F}. \vec{dr} = \int \int_S (\nabla \times \vec{F}).\vec{dS}$

Also, learn how to solve differentiation under the integral sign if the integral depends on a variable and a parameter.

Applications of Stoke’s Theorem

Stoke’s theorem has a wide range of applications in mathematics and physics. Some of these are listed below:

• Stoke’s theorem is used to calculate the flux of a vector field through a surface by using the curl.
• It is a fundamental theorem to derive and understand conservation laws. For example, in fluid mechanics, it is used to derive conservation laws of mass, momentum, and energy.
• In electromagnetism, it is used to derive Maxwell’s equations and to solve boundary value problems.
• This theorem is used to prove the conservation of angular momentum in rotational systems.

Conclusion

In calculus, Stoke’s theorem is a fundamental theorem that relates a line integral of a closed curve with the surface integral of the curl of a vector field containing the surface. It has a wide range of applications in mathematics and physics. It is also known as the generalization of Green’s theorem which is also another fundamental theorem of calculus.